Abstract
Background: Tradeable credit assets are vulnerable to two varieties of credit risk: default risk (which manifests itself as a binary outcome) and spread risk (which arises as spreads change continuously). Current (2017) regulatory credit risk rules require banks to hold capital for both these risks. Aggregating these capital amounts is non-trivial.
Aim: The aim was to implement the bubble value at risk (buVaR) approach, proposed by Wong (2011) to overcome the risk aggregation problem. This method accounts for diversification and for procyclicality and operates by inflating the positive side of the underlying return distribution, in direct proportion to prevailing credit spread levels (usually liquid credit default swap spreads).
Setting: The principal setting for the study was the South African credit market which represents a developing market. Previous work by Wong (2011) focussed only on developed markets.
Methods: Using South African data, closed form solutions were derived for free parameters of Wong’s formulation, and the relationship between the spread level and the response function was developed and calibrated.
Results: The results indicate that the original calibrations and assumptions made by Wong (2011) would result in excessive capital requirement for South African banks. Estimates obtained from this work suggest further calibration is required to cover the unique features of the South African milieu. Considerable differences compared with other markets were also found.
Conclusion: The application of buVaR to South African government bond credit default swaps spreads highlighted the metric’s countercyclical properties that would potentially have countered bubble developments had they been implemented during the credit crisis of 2008/2009. Regulatory authorities should take this important metric into account when allocating South African bank’s credit risk capital.
Introduction
Credit losses experienced in the financial crisis of 2008–2009 emphasised the complexities surrounding tradeable credit instruments. In their fundamental review of the trading book, the Basel Committee on Banking Supervision (BCBS 2013) asserted that credit-related products had been a major source of losses and the approach and treatment of these positions were severely flawed. The crisis also prompted financial institutions to change their evaluation and management of credit risk substantially (BCBS 2015).
A 2013 global survey conducted by the Joint Forum on Banking Firms and Supervisors revealed that since the crisis banks have improved governance and risk reporting and that risk aggregation has become far more sophisticated (BCBS 2015). Modelling enhancements driven by regulatory requirements stress testing and crisis experience has significantly shifted institutions’ reliance to internal models as the ‘search for yield’ intensifies in a post-crisis low interest rate environment (BCBS 2015). Despite these promising developments, the BCBS has attempted to align the requirements of the trading book1 more closely with those of the banking book (BCBS 2013). The BCBS (2013) proposes substantial revisions to many aspects of the treatments of market risk – these have now (2018) been reviewed by market participants and approved for implementation (BCBS 2014).
In the trading book, tradeable credit instruments are associated with two sources of risk. Firstly, default risk in which there is a probability that the underlying issuer may forfeit its obligation through contractual non-compliance (Brown & Moles 2014) and, secondly, spread risk in which losses arise from changes in an instrument’s credit spread. This spread can be defined as the instrument’s yield relative to that of a comparable-duration default free instrument and is not attributable to defaults or credit migrations (BCBS 2009). The complicated relationship between credit and market risk and the aggregation of these risks are emphasised by the fact that approximately two-thirds of financial crisis (2008–2009) losses were attributable to spread risk with only a third of the losses stemming from actual defaults (BCBS 2011). Sophisticated financial instruments based on securitisation played a pivotal role in the financial crisis masking risk and increasing the interconnectedness of financial markets. A downward spiral of the quality of the securities backing these instruments caused several rating downgrades of these instruments and precipitated chaos within globally interconnected financial markets. Further, the procyclical nature of these markets, albeit contributing significantly to the pre-crisis market euphoria, fuelled one of the biggest busts in financial history (Bank for International Settlements 2008; Papaioannou et al. 2013).
Procyclicality – defined as those economic quantities that are positively correlated with the overall state of the economy (Van Vuuren 2012) – leads to institutions reducing lending capacity throughout market busts. Regulatory capital models using data from busts would recommend banks keep higher levels of capital as well (this is also influenced by stress testing of models); the opposite is true in financial booms. This procyclical characteristic of markets, methods and metrics has been countered by the introduction of the countercyclical capital buffer (CCB) by the BCBS in 2010 which is based on the aggregate credit-to-GDP gap ratio (BCBS 2010). The buffer is mostly untested in emerging and developing markets and thus the complexities regarding its implementation and timing have not been comprehensively divulged.
Value at risk (VaR) has been the preferred market risk measurement tool since 1994 (BCBS 1994), but suffers from significant shortcomings, many of which played a significant role in the crisis. These problems were partially ameliorated by the replacement of VaR with expected shortfall (ES) in 2018 (BCBS 2013). Although VaR is relatively simple to calculate, it does not account for risk aggregation and is also procyclical in nature. Further, VaR models used in credit risk measurement are mostly dependent on regulatory information such as rating transition matrices making these models slow to reflect current market conditions. ES solves some of VaR’s shortcomings as it embraces not only the likelihood of losses, but also the size of losses beyond the VaR confidence level, thus accounting for risk in a more comprehensive manner (BCBS 2013). However, procyclicality remains an issue as ES uses the same historical data produced by markets as VaR does. This necessitates the use of a CCB. However, further analysis of the proposed buffer components has suggested alternatives to the credit-to-GDP gap. The research includes that of Barrell et al. (2010), Shin (2013) and Behn et al. (2013) who all proposed alternatives to this metric. Drehmann and Tsatsaronis (2014) review these studies and argue that the credit-to-GDP gap is the best standalone early warning indicator over forecast horizons of 2 to 5 years. They further find that the debt service ratio (DSR) is the best single indicator for forecast horizons shorter than 2 years. Drehmann and Tsatsaronis assert that both judgement and quantitative analysis are required by policymakers as there are no foolproof models that provide an effective rule-based countercyclical measure. Further, although the credit--to-GDP gap ratio was found to be optimal, Drehmann and Tsatsaronis found that a combination of other indicators may work better for certain jurisdictions.
Applying conventional VaR to tradeable credit instruments poses challenges, as all the risks pertaining to these instruments are not adequately captured in the measurement (Amato & Remolona 2003; Elton et al. 2001). Further, under the Basel Market Risk framework, it is also not a requirement to measure multiple risks in one model. Spread and default risk are currently simply added together after being individually measured without accounting for diversification possibilities as prescribed. Although aggregation issues present problems regarding diversification and even compounding of risks, Wong’s (2011) bubble VaR (buVaR) proposes a unified method of combining these two forms of risks avoiding the problem of risk aggregation. Further, the model relies on credit spread data avoiding transition matrices or ratings information. Credit default swap (CDS) data are forward-looking and highly liquid as they are readily available daily (Huang, Zhou & Zhu 2009). Using these data, Wong illustrates the asymmetry between defaults and spread movements and asserts that spread widening will always precede defaults. Although Wong calibrated the buVaR credit risk model for several countries, South Africa was not among them. This article explores that calibration, estimates potential standardisation and provides deeper insight into the model’s applications in the South African milieu.
The remainder of this article proceeds as follows: the ‘Literature study’ section explores tradeable credit instruments and the regulatory treatment thereof. The section also highlights difficulties in the measurement of credit risk under regulatory recommendations. The choice of data and relevance thereof is explained in ‘Data and methodology’ section along with the mathematics of the metrics being assessed. The logic behind Wong’s (2011) credit buVaR and how the metric may sufficiently account for diversification possibilities when spread and default risk are combined into one metric are also discussed here. Results obtained from analysis and scenario simulations are then illustrated and discussed in the next section and the final section concludes.
Literature study
Regulatory treatment of tradeable credit instruments
Conventionally, a bank’s trading book is predominantly affected by market risk, with the banking book being mostly susceptible to credit risk (BCBS 2009). However, tradeable credit instruments introduce credit risk to the trading book and the regulatory capital calculated for these in the crisis were woefully insufficient. These tradeable credit instruments do, however, provide for price discoveries in secondary markets through credit spreads.
Institutions holding portfolios of debt securities or derivatives to hedge risk stemming from their securities, face several forms of risk. Spread movements is one such risk, while the possibility of issuer defaults of tradeable credit instruments is another. Correlated defaults between issuers of securities pose further risk to banks and financial institutions (Wong 2011).
Spread risk
Spread risk is traditionally modelled using historical simulations and applying a VaR approach. Simulated returns are generated from the spread variable over an observation period – between 1 and 3 years under the Basel formulation. The return vector is  and each portfolio position is mapped to benchmark issuer risk factors, so if the portfolio is subject to N risk factors, there are N return vectors. Return vectors are combined to derive a portfolio profit and loss distribution. Under the Basel II formulation, spread VaR is the VaR over a 10-day period at a 99% confidence level as it is for standard market risk instruments and portfolios (BCBS 1994). and each portfolio position is mapped to benchmark issuer risk factors, so if the portfolio is subject to N risk factors, there are N return vectors. Return vectors are combined to derive a portfolio profit and loss distribution. Under the Basel II formulation, spread VaR is the VaR over a 10-day period at a 99% confidence level as it is for standard market risk instruments and portfolios (BCBS 1994).
In what has been informally labelled Basel IV, the BCBS have suggested changes to the trading book/banking book boundary by addressing issues such as the trading book definition, trading book components and ineligible trading book instruments (BCBS 2013). Such rigorous proscriptions were limited to mere footnotes in the revisions of the Basel II market risk framework (BCBS 2011) – now, they have become standard features of the way banks will need to treat trading books. A summary of the current boundary definitions compared to proposals are highlighted in Table 1.
| TABLE 1: Boundary definitions of Basel II and Basel IV trading book. |
Default risk
Because entities only default once, an historical simulation approach is impossible since there is no time series of observable default history available. Monte Carlo simulations are used instead. Possible occurrences of ratings migration (of which default is a special case) are generated over a 1-year simulation horizon. The Monte Carlo simulation assumes that credit default driver follows a particular distribution: simulated values are mapped to an end-state rating (upgrades, downgrades or a default). The probabilities of these trajectories from the current rating to the end-state ratings (including default) are embedded within the rating transition matrix. These matrices are populated with single-year transition rates assembled by credit rating agencies using empirical historical statistics of defaults and upgrades or downgrades in selected benchmark sectors. The portfolio positions are mapped to relevant sectors before the simulation begins. Correlation coefficients are determined independently and used to capture correlation risk between the sectors. Regulatory capital rules require that the VaR of this distribution is determined at a 99.9% confidence level and a time horizon of 1 year – this is known as credit VaR. Crouhy, Galai and Mark (2000) provide a comprehensive overview of contemporary, available credit risk models.
The responses received by the BCBS from commentators mostly suggested that integrating the default component of the trading book into market risk models, presents several challenges and complexities. The BCBS thus decided that the total credit risk capital charge for both the standardised and models-based approaches would comprise two components: an integrated credit spread risk capital risk charge and an incremental default risk (IDR) charge (BCBS 2013).
Aggregation problems
The complex relationship between market and credit risk gives way to aggregation issues including the inability to clearly identify diversification issues and related compounding effects. This challenge also fuelled the perception that adding separately estimated risk components for market and credit risk will most certainly be conservative, due to not all diversification possibilities being considered. However, the BCBS suggests from the financial crisis learnings that non-linear interactions between market and credit risk may reinforce each other and lead to even more severe losses. The BCBS further suggests that under a top-down aggregation approach (as commonly used in practice) diversification benefits should be approached with caution (indeed, the BCBS now restricts the use of negative correlations in portfolio assembly and construction, BCBS 2013).
Adding independently estimated risk measurements in a top-down approach is flawed in that it assumes that perfect correlations between market and credit risks exist. Since both risk forms are affected by the same economic factors, some diversification benefits are expected. However, non-linear interactions between market and credit risk may lead to instances where the combined total risk is higher than the sum of individually measured components.2 These compounding effects often arise when market and credit risks are inseparably connected, that is, default losses from instruments depend on the movements in market risk factors or conversely when the values of instruments affected by market risk factors are dependent on defaults or rating changes.
Diversification benefits are, however, not unobtainable and the BCBS highlights this by showing the interactions between interest rates and credit risk in the banking book. Creating a hypothetical bank, Drehmann, Sorensen and Stringa (2008) place emphasis on modelling the entire banking book including assets, liabilities and interest sensitive off-balance sheet items. Drehmann et al. argue that non-linear effects created by the interaction between interest rates and default probabilities may be difficult to capture outside of integrated models measuring total risk. Alessandri and Drehmann (2007) further assess aggregate risk and required capital by using a set of stylised assumptions to calibrate the model to the profile of a typical UK bank. Through this they show diversification benefits such that the capital kept for an integrated risk measurement for interest rate and credit risk is less than would have been kept for credit risk if measured separately.
Diversification benefits are not guaranteed when using VaR, since the market risk measure is neither coherent nor sub-additive. Coherent risk measures such as ES guarantee the diversification benefits if an integrated measurement of total risk is measured. If separate measurements are done for market and credit risk, diversification benefits cannot be guaranteed even if coherent measurements are used. The choice of metric is not the only challenge related to integrated risk measurement. The metrics used in credit and market risk are not entirely comparable. For example, market risk models capture complete return distributions whereas credit risk models account mostly for losses stemming from defaults and ignore gains. A further challenge emerges in the different horizons that the risks are measured in, despite credit risk becoming more tradeable in the 21st century because of financial innovations such as securitisation.
The BCBS conclude that although integrated risk models have high data and technological demands, the aggregation and integrated measurement of market and credit risk should be done consistently in such a way that a common horizon is imposed, and all income, profits and losses are accounted for. However, the challenges mentioned, as well as the fact that a top-down approach is favoured by most banks with these approaches involving simple correlations ignoring non-linear interactions, suggest that even under integrated measurements diversifications benefits are not guaranteed.
Data and methodology
Data
The data employed in the credit buVaR risk metric were daily credit spreads for 5-year and 10-year South African government CDSs, from January 2000 to November 2016. South African credit ratings were obtained from Fitch ratings (Fitch Ratings 2016). The South African risk-free rate (3-month Johannesburg Interbank Agreed Rate [JIBAR]) used in this analysis is sourced from the South African Reserve Bank (SARB 2016). Other data were simulated where necessary.
Methodology
Spread risk
Credit buVaR combines both spread and default risk and Wong (2011) asserts that the all-in credit loss measure lies between spread VaR and a logical upper bound. This upper bound represents the default event where the difference between the principal amount and the recovery is lost. Spread VaR is thus calculated as usual, but the inflator allows default risk to also be accounted for.
Default risk
Compared with conventional default risk measures, the way in which default risk in the credit buVaR model is accounted for contrasts with spread VaR. The reliance on slow-reacting, backward-looking rating transition matrices is entirely replaced by the derivation of the cap on the spread level used in the subsequent inflator. This inflator imposed on the spread VaR measurement ensures a forward-looking, all-in credit loss measurement.
Aggregation problems
The credit buVaR model allows for credit and market risks in a diversifiable manner while solely relying on credit spread data. Wong (2011) asserts that credit spread is the most forward-looking and direct indication of an issuer’s probability to default. Wong also suggests that rapid spread widening (RSW) is the dominant forerunner for default and presents evidence from the financial crisis. Using data from issuers including Lehman Brothers and American International Group (AIG), Wong illustrates how spreads throughout the crisis period increased to such an extent that potential default could be detected weeks earlier than if relying on credit VaR alone. Through this Wong deduced that a credit model conditional on RSW could be forward-looking and may overcome shortcomings of conventional credit models.
This straightforward method using an historical simulation approach does not produce a statistically precise method, but neither do other VaR approaches (Wong 2011). Credit buVaR, like other VaR approaches, is affected by the subjective choice of parameters and has a free parameter calibrated by the user.
Credit buVaR’s ability to account for both default and spread risk in one regulatory capital calculation is made feasible when the calculation metric aims to detect widening of the issuer’s credit spreads. Wong (2011) suggests that credit spreads are arguably one the most direct and forward-looking measures of an issuer’s default probability. To penalise increasing default probability Wong asserts that an inflator (Δ+) is used to increase the VaR measure as required.
Since increased spreads precede defaults, long positions incur losses due to these changes while negative changes in spreads cause losses for short positions. However, defaults only affect long positions and thus the inflator is only applied to the positive side of the distribution. To incorporate the inflator the original return distribution undergoes a transformation when the returns are positive as shown in Equation 1.
In Equation 1, the inflator (Δ+) is always greater than 1, so it amplifies the positive returns (positive returns in this case represent an increase in spreads which represent a loss scenario), and n is the scenario numbers in the historical VaR simulation. Wong (2011) proposed the inflator in Equation 2 to rapidly penalise the initiation of RSW:
S is the benchmark CDS spread while ω1 and ω2 are free parameters. A pricing function is used to cap the inflator as spreads cannot widen indefinitely without the benchmark bond entering default at some stage. Wong (2011) suggests that the pricing function such as that from an Excel spreadsheet will suffice: Yield = (today, maturity, coupon rate, bond price, redemption price coupon frequency).
To calculate the spread cap, Scap, Wong (2011), using the Lehman Brothers bankruptcy as a guide, assumes that the recovery rate in the event of a default will be 10%. Most bonds are assumed to be issued close to par when the outlook of the issuing company is attractive, so much so that the coupon rate can be set to (or close to) the risk-free rate. The final assumption is that bonds give the same quarterly cash flows like a CDS, to be consistent with CDS quotes. The assumptions allow for the spread of the bond at the point of default to be stated as:
Ydefaulted is the yield of the bond at the point of default. Wong (2011) illustrates a basic example on how to perform this calculation using a standard discounted pricing function (e.g. the yield function in Excel outlined above) and defines the maximum inflator (Δ+) as an adjustment that will inflate two standard deviations of spread returns up to the percentage loss at the point of default, calculated as Scap. This two standard deviation in Equation 4 represents a 97.7% VaR under a normal distribution (chosen because it simplifies the formulation; in principle, any level would suffice).
However, Scap satisfies Equation 3, thus:
Substituting into Equation 2 produces the response function:
Equation 6 still has the free parameter ω2 which must be calibrated. Wong (2011) argues that ω2 = 0.5 is the most suitable as it produces an inflator that increases rapidly to penalise RSW; however, it decreases in such a way that the spread inflated through the inflator will never exceed Scap. This ensures that the holder of the bond will never lose more than the principal amount, less the recovery amount. An advantage of ω2 as a free parameter is that it can be adjusted and calibrated as required by a regulator, depending on the requisite level of conservatism.
Results and discussion
Current (2018) South African milieu
The credit buVaR model relies integrally on the simulation of Scap indicating the moment of default. This is fundamental to the model as it enables the aggregation of spread and default risk. Central to Scap is the risk-free rate of the market as well as the assumed bond recovery rate in the event of default. Firstly, compared with the US, South Africa is a high interest rate environment and thus the risk-free rate used to calibrate Scap is considerably elevated. JIBAR (November 2016) is used as the risk-free rate for calibration. In addition, the lack of CDS data for the South African market complicates the assumption of a recovery rate, since no noteworthy government or corporate bonds for which there are CDS data defaulted in the analysis period.
Simulation results – Calibration assumptions
Figure 1 shows the performance of spread VaR and credit buVaR relying on VaR for the calculation of credit buVaR on SA 5-year government bond CDS spreads. Figure 1 assumes the same recovery assumption (10%) and more importantly the same ω2 = 0.5 as that of Wong (2011). The risk-free rate has, however, been calibrated for South Africa.
 |
FIGURE 1: Credit risk measures on 5-year credit default swap spreads using standard deviation as a measure of volatility (risk-free rate = 7.00%, bond recovery rate = 10%, ω2 = 0.5). |
|
The uncalibrated buVaR output in Figure 1 shows significantly elevated capital estimations compared to spread VaR throughout the observation period. The purpose of buVaR, as a countercyclical measure, is to assist banks in their determination of the ‘correct’ amount of credit risk capital during different stages of the business cycle. However, capital requirements under buVaR are excessive and would require institutions to keep between two and seven times more capital than measured using conventional VaR (as observed during the observation period indicated in Figure 1), placing an onerous burden on capital requirements and diverting liquidity to less-profitable operational areas. This highlights the necessity of appropriate model parameter calibration.
Wong (2011) advised that each jurisdiction should calibrate its own model input parameters. For the South African market, a bond recovery rate of 50% was assumed (J. Esterhuysen pers. comm., 2016) – far more than the 10% used in Wong’s (2011) exposition. South Africa’s historical experience of corporate defaults has been less detrimental than that faced in developed economies, partially due to the stringency of the National Credit Act which curtailed institutions’ reckless lending activities (SA NCA 2005).
The bond recovery rate assumption is implemented first as it is based on empirical market data and insight, whereas the free parameter ω2 is calibrated to a suitable level and chosen at the discretion of the user. A ω2 of 1.0 (c.f. Wong 2011: ω2 = 0.5) reduces the increase of buVaR over conventional VaR to levels that may be acceptable to banks: between 1.0 and 2.5. Figure 2 illustrates a calibrated buVaR model output based on assumptions for the South African market.
 |
FIGURE 2: Credit risk measures on five-year credit default swap spreads using standard deviation as a measure of volatility (risk-free rate = 7.00%, bond recovery rate = 50%, ω2 = 1.0). |
|
Assuming better bond recovery rates and applying a larger ω2 produces results that are still elevated – but more sensible using buVaR – as shown in Figure 2. The spike in CDS spreads in 2015 was a direct result of the political instability (which led to economic instability) caused by the removal of the Minister of Finance (Nhlanhla Nene) in December 2015. Subsequently, rating agencies warned of further downgrades – possibly to junk status – still faced by the country (Moody’s Investor Services 2016).3 Figure 3 concentrates on the crisis period from Figure 2 and shows the elevated capital requirements (which would have been required under the buVaR metric). This reinforces buVaR’s countercyclical objective.
 |
FIGURE 3: Credit risk measures on five-year credit default swap spreads using standard deviation as a measure of volatility in the months preceding the credit crisis. Arrows indicate focus regions. |
|
Figure 3 illustrates the end of the non-volatile pre-crisis period and subsequent crisis period in which spreads increased significantly. BuVaR reacts more quickly and to a greater extent than spread VaR to what Wong (2011) described as ‘rapid spread widening’. This results in a quicker increase in capital requirements which further motivates the use of buVaR because of its potential countercyclical capabilities. Both indicated areas might have curbed rapid expansion and potentially avoided bubble formation. Estimating these higher capital requirements cannot be back-tested, so hindsight does not offer much benefit.
The choice of volatility measure may influence buVaR’s suitability. It is well known that better, more reactive measures of volatility are frequently used in practice, such as generalized autoregressive conditional heteroskedasticit (GARCH) and exponentially weighted moving average (EWMA) models. Figure 4 shows spread VaR and buVaR using an EWMA volatility methodology. The difference in required capital under an EWMA volatility approach and a standard deviation volatility approach (Figure 2) is not material.
 |
FIGURE 4: Credit risk measures on five-year credit default swap spreads using the EWMA approach as a measure of volatility (ω2 = 1.0, λEWMA = 0.95). |
|
Calibration of required parameters to South African market
The EWMA approach in Figure 4 places reliance on more recent data when estimating volatility. Credit buVaR and spread VaR provide more reactive measurements to time series changes under EWMA.
The choice of VaR measure may also influence buVaR’s suitability. Despite VaR being widely used in finance, the BCBS has decided to replace it with ES or ‘conditional VaR’ (BCBS 2013). Recall that the ES – the probability-weighted average of losses beyond a specified value of VaR – is calculated as follows:
σ is the portfolio standard deviation and α is the VaR value beyond which the ES is desired. The two metrics were used in the buVaR model and the results are compared in Figure 5.
 |
FIGURE 5: Credit bubble value at risk using value at risk and expected shortfall. |
|
Figure 5 illustrates that buVaR using ES is more reactive than buVaR using conventional VaR. ES provides a more conservative measure compared with spread VaR because it considers not only the likelihood of losses, but also their magnitude, leading to a more coherent measure. This is illustrated by the severe fluctuations of ES buVaR in the post-crisis period because ES measures the loss severity, while VaR provides an estimate of loss frequency.
Figure 6 applies the buVaR model to 10-year South African government bond CDS spreads. The calibration of ω2 (= 1.0) remains identical to that chosen for five-year South African government bond CDS spreads as this value produces similar capital retention levels (c.f. Figure 2).
 |
FIGURE 6: Credit buVaR for 10-year credit default swap spreads (risk-free rate = 7.00%, bond recovery rate = 50%, ω2 = 1.0). |
|
Figure 7a illustrates the effect of changing spread levels, S, on the inflator, Δ+. Each line represents Δ+ versus S at various ω2 values (these ω2 values are the numbers on the graph at the maximum value of Δ+ for each fixed ω2). Figure 7b shows the spread after application of Δ+ versus the current spread, S. See Equation 4.
 |
FIGURE 7: (a) The effect of the spread level, S, on ∆+ (as well as an indication of the maximum ∆+ for different levels of ω2 and (b) the effect of spread level, S, on value at risk for various levels of ω2. |
|
The first derivative of Equation 6 (see Appendix 1) gives the rate of change of Δ+ with respect to S. Setting this derivative to 0 determines the value of S where Δ+ is a maximum (i.e. the open circles in Figure 7a).
Lower ω2 values generate inflators which elevate spreads early, that is, far from levels at which the bond would default. Wong (2011) asserted that Δ+ should penalise excessive growth as soon as possible and thus applies an ω2 = 0.5. Higher ω2 values elevate spreads more slowly than lower ω2 values, so excess growth is only penalised severely enough at spread levels close to those that would result in a bond default.
Figure 8 shows a surface plot of Δ+ for various levels of ω2 and S.
 |
FIGURE 8: Surface plot showing the impact of ω2 and spread level, S, on ∆+. |
|
Figure 8 illustrates the importance of calibrating the buVaR model for the market to which it is applied. As shown in Figure 1, Wong’s (2011) ω2 value of 0.5 would apply too harsh a capital requirement for institutions as buVaR is five times higher than spread VaR during crisis periods. This quantity of capital retention would be too punitive for most institutions. At low ω2 values, the inflator imposes severe liquidity constraints on institutions. A higher ω2 is thus preferred in this study. Using Figure 8, the inflator can be calibrated to the bank’s relevant, acceptable value.
Figure 9 illustrates the rate of change of the Δ+ (its first derivative) with respect to S.
 |
FIGURE 9: First derivative of ∆+ with respect to spread level, S. |
|
The rate of change of Δ+ is considerably elevated in the pre-crisis period. This highlights the model’s ability to anticipate market bubbles and subsequently elevate buVaR through Δ+ to potentially retard or halt the bubble’s development.
Figures 10a and b illustrate the effects of model components, rf , and the assumed bond recovery rate on Scap.
 |
FIGURE 10: Impact of (a) the risk-free rate on the inflator as a function of S and (b) the bond recovery rate on Scap. |
|
An increase in rf increases Scap as well as the value of S at which Δ+ experiences a maximum. Using Equation 3, as rf increases, the yield at default, Ydefaulted, increases at a faster rate, so Scap = Ydefaulted − rf increases. This influence is trivial compared with the impact of the recovery rate on Scap (Figure 10b). Low recovery rates result in dramatically elevated levels of Scap.
Denzlera et al. (2006) showed that probabilities of default could be derived from credit spreads using:
S is the credit spread level in basis points, t is the maturity of the CDS in years, PD is the probability of default and LGD is the loss given default of the CDS instrument – both expressed as percentages. ETF (2011) showed Equation 8 could be approximated using:
Figure 11 illustrates the market-implied PD’s as derived using Equation 9 in conjunction with the South African credit rating (supplied by Fitch Ratings) and the five-year CDS spreads.
 |
FIGURE 11: Market-implied probabilities of default (using Equation 9 and five-year credit default swap spreads from Figure 1), South African credit rating (mapped to relevant probability of default) and bubble value at risk on the same timescale. |
|
South Africa’s credit rating is currently (November 2016) just above junk and has a negative outlook (Moody’s Investor Service 2016) as shown in Figure 11. This suggests that political actions (removal of Minister Nene), rather than only market-implied PDs, weigh heavily on the opinions and confidence of rating agencies. Were only the latter considered, the current lower spreads (relative to credit crisis levels) imply that South Africa should be assessed at a better (higher) credit rating. Unsurprisingly, there is a strong correlation between credit buVaR (using data from Figure 1) and market-implied annual PDs.
Consequences for South African banks and regulators
Implementation of a buVaR-like model in the banking environment would require significant cooperation between the regulator and regulated institutions. Bubble VaR models effectively attempt to replace the BCBS countercyclical buffer and thus thresholds and parameters would have to be tested and agreed upon. What would be an evident advantage of such a model is that it would not be burdened by complicated timing issues regarding the retention and release of capital buffers. These timing issues under the current BCBS formulation would be a key focus area, as they would have to be analysed and compared with continuous capital estimates under buVaR models.
Initial research between regulators and banks could focus on the optimal value for ω2, as a comparison of this work with Wong’s (2011), shows considerably different results for different values of this parameter. This research could analyse banks’ portfolios to ensure that the model would perform consistently across the market. In jurisdictions where data are scant for both CDS spreads and historical defaults, regulators would have to cooperate with market experts on defaults and recovery assumptions. Wong (2011) highlighted that under a buVaR model environment there would be macro-prudential advantage in that institutions not affected by buVaR capital requirements could price more competitively, thereby transferring credit risk from the banking sector to other global investors as well.
Conclusions and suggestions for future work
Regulatory capital recommendations for financial markets are constantly evolving. A combination of several BCBS publications4 has been informally labelled as Basel IV (Nooman 2016). These recommendations aim to regulate the banking environment where complex interconnected financial instruments have historically masked risk and exhibit considerable measurement complexity. Wong’s (2011) buVaR model provides a risk metric combining both spread and default risk. Relying on liquid forward-looking CDS spread data, the model bypasses the problem of risk aggregation by employing a single model under the historical VaR/ES approach. Wong (2011) stressed that, like all VaR approaches, the model is influenced by subjective choices of parameters and thus does not provide a statistically precise measurement. This emphasises the necessity for regulators and banks to cooperate to ensure the ‘correct’ parameters are used in their jurisdiction.
Bubble VaR results using Wong’s (2011) original calibrations and assumptions, illustrate excessive capital requirement estimates and suggest further calibration requirements. A higher bond recovery assumption after default and a higher ω2 produces more feasible estimates. Applying buVaR to 5 and 10-year South African government bond CDS spreads produced results showing that buVaR is more responsive and conservative prior to periods of severe CDS spread increases. This highlights the metric’s countercyclical properties that would potentially have countered bubble developments. Depicting buVaR results on the same timescale as market-implied PDs and the South African credit rating shows that buVaR does ramp up significantly in the pre-crisis bubble development period. However, the model is robust when shocks occur such as the removal of the Minister of Finance in late 2015.
A tractable solution is provided in Equation 2-A1, which simplifies the selection of the free parameter, ω2. Within any jurisdiction, institutions and policymakers will have local knowledge of bond recovery and risk-free rates which, in turn, determine Scap Using this information in conjunction with the results from Equation 8, the inflator level can be quickly calculated for any ω2 and, thus, the associated increase in capital can be ascertained. This can be used as a guide for regulatory and institutional capital calibration.
The procyclical nature of financial markets and the way in which its participants react to fuelling this phenomenon are well documented. The BCBS proposed the implementation of a CCB, but this has raised concerns regarding uncertainty whether the right data are used for estimation: the credit-to-GDP ratio may not be optimal for jurisdictions with unique markets (Drehmann & Tsatsaronis 2014). Further timing issues are a concern as capital for the buffer can be released immediately, but retention notices must optimally be made 12 months in advance. The credit buVaR model provides a continuous forward-looking metric that is not burdened by timing issues and is not subject to procyclicallity, as it does not rely on credit ratings or transition matrices.
Future research opportunities include the optimal calibration of the free parameter ω2. This parameter has a significant impact on the buVaR model and appropriate guidance is required if it is to be implemented. Research on the parameter would include analysis across multiple economies, markets and scenarios to ensure suitable implementation guidelines are created. Further research may also include investigation on the relationship between model outputs, CDS spreads and actual credit ratings as it was not the central focus of this study. Finally, as capital requirements for tradeable credit instruments arise both from default and spread risk, further research may analyse combined capital requirements from separate conventional models to that of aggregating buVaR-like models.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors’ contributions
D.V. was the principal author and analyst and G.v.V. responsible for model design and implementation of the article.
References
Alessandri, P. & Drehmann, M., 2007, An economic capital model integrating credit and interest rate risk in the banking book, Working Paper No. 1041, April 2009, European Central Bank, Frankfurt.
Amato, J.D. & Remolona, E.M., 2003, ‘The credit spread puzzle’, BIS Quarterly Review 2003, 51–63. https://doi.org/10.2139/ssrn.1968448
Bank for International Settlements, 2008, Addressing financial system procyclicality: A possible framework, Note for the FSF Working Group on Market and Institutional Resilience, viewed 11 November 2016, from http://www.fsb.org/wp-content/uploads/r_0904e.pdf?page_moved=1
Barrell, R., Davis, E., Karim, D. & Liadze, I., 2010, Calibrating macroprudential policy, NIESR Discussion Papers, no 354, National Institute for Economic and Social Research, London.
BCBS, 1994, Overview of the amendment to the capital accord to incorporate market risks, viewed 15 June 2016, from https://www.bis.org/publ/bcbs23.htm
BCBS, 2009, Guidelines for computing capital for incremental risk in the trading book – Consultative document, viewed 12 June 2016, from http://www.bis.org/publ/bcbs149.pdf
BCBS, 2010, Guidance for national authorities operating the countercyclical capital buffer, viewed 01 June 2016, from http://www.bis.org/publ/bcbs187.pdf
BCBS, 2011, Capital treatment for bilateral counterparty credit risk finalised by the Basel Committee – Press release, viewed 13 Jun 2016, from http://www.bis.org/press/p110601.htm
BCBS, 2013, Fundamental review of the trading book: A revised market risk framework, viewed 22 October 2016, from http://www.bis.org/publ/bcbs265.pdf
BCBS, 2014, Fundamental review of the trading book: Outstanding issues – Consultative document, viewed 22 October 2016, from https://www.bis.org/bcbs/publ/d305.htm
BCBS, 2015, Interest rate risk in the banking book – Consultative document, viewed 01 June 2016, from http://www.bis.org/bcbs/publ/d319.pdf
Behn, M., Detken, C., Peltonen, T. & Schudel, W., 2013, Setting countercyclical capital buffers based on early warning models: Would it work?, Working Paper No. 1604, November, European Central Bank, Frankfurt.
Brown, K. & Moles, P., 2014, Credit risk management, viewed 01 Jun 2016, from https://www.ebsglobal.net/EBS/media/EBS/PDFs/Credit-Risk-Management.pdf
Crouhy, M., Galai, D. & Mark, R., 2000, ‘A comparative analysis of current credit risk models’, Journal of Banking and Finance 24(1–2), 59–117. https://doi.org/10.1016/S0378-4266(99)00053-9
Denzlera, S.M., Dacorognaa, M.M., Müllera, U.A. & McNeil, A.J., 2006, ‘From default probabilities to credit spreads: Credit risk models do explain market prices’, Finance Research Letters 3(2), 79–85. https://doi.org/10.1016/j.frl.2006.01.004
Drehmann, K. & Tsatsaronis, K., 2014, ‘The credit-to-GDP gap and countercyclical capital buffer: Questions and answers’, BIS Quarterly Review March, viewed 15 November 2016, from http://www.bis.org/publ/qtrpdf/r_qt1403g.pdf
Drehmann, M., Sorensen, S. & Stringa, M., 2008, The integrated impact of credit and interest rate risk on banks, Bank of England Working Paper, 339, viewed 01 Jun 2016, from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=966270
Elton, E.J., Gruber, M.J., Agrawal, D. & Mann, C., 2001, ‘Explaining the rate spread on corporate bonds’, The Journal of Finance 56(1), 247–277. https://doi.org/10.1111/0022-1082.00324
ETF, 2011, Market-implied default probabilities and credit indexes. ETF.com., viewed 08 September 2016, from http://www.etf.com/publications/journalofindexes/joi-articles/10605-market-implied-default-probabilities-and-credit-indexes.html
Fitch Ratings, 2016, Fitch affirms South Africa at BBB-, viewed 15 November 2016, from https://www.fitchratings.com/site/pr/1005740
Huang, X., Zhou, H. & Zhu, H., 2009, A framework for assessing the systemic risk of major financial institutions. Finance and Economics Discussion Series, Division of Research & Statistics and Monetary Affairs, Federal Reserve Board, Washington, DC, viewed 22 September 2016, from https://www.federalreserve.gov/pubs/feds/2009/200937/200937pap.pdf
Moody’s Investor Service, 2016, Moody’s confirms South Africa’s sovereign rating at Baa2, viewed 19 September 2016, from https://www.moodys.com/research/Moodys-confirms-South-Africas-sovereign-rating-at-Baa2-and-assigns--PR_348291
Nooman, L., 2016, ‘Basel IV spectre looms for battle-worn bankers’, Financial Times, 14 March, viewed 15 November 2016, from https://www.ft.com/content/a9d6eb94-ce5d-11e5-831d-09f7778e7377
Papaioannou, M.G., Park, J., Pihlman, J. & Van der Hoorn, H., 2013, Procyclical behaviour of institutional investors during the recent financial crisis: Causes, impacts, and challenges, WP/13/193, Monetary and Capital Markets Department, International Monetary Fund, Washington, DC.
PWC, 2016, Basel IV at a glance, viewed 15 November 2016, from http://www.pwc.com/gx/en/services/advisory/basel-iv.html
SA NCA, 2005, South African National Credit Act 34 of 2005, viewed 22 October 2016, from http://www.justice.gov.za/mc/vnbp/act2005-034.pdf
SARB, 2016, South African Reserve Bank, viewed 15 November 2016, from https://www.resbank.co.za/Research/Rates/Pages/CurrentMarketRates.aspx
Shin, H.S., 2013, Procyclicality and the search for early warning indicators, WP/13/258, International Monetary Fund, Washington, DC.
Van Vuuren, G., 2012, ‘Basel III countercyclical capital rules: Implications for South Africa’, South African Journal of Economic and Management Sciences 15(3), 309–324. https://doi.org/10.4102/sajems.v15i3.235
Wong, M., 2011, ‘Credit BuVaR: Asymmetric spread VaR with default’, Journal of Risk Management in Financial Institutions 5(1), 86–95. https://doi.org/10.2139/ssrn.1627689
Appendix 1
First derivative of Equation 6:
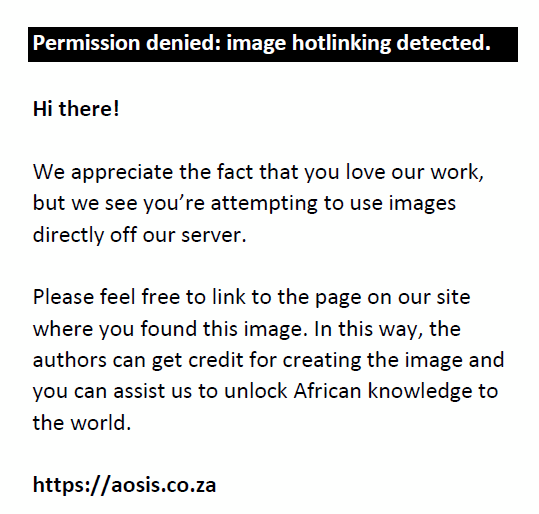
This function = 0 (since when 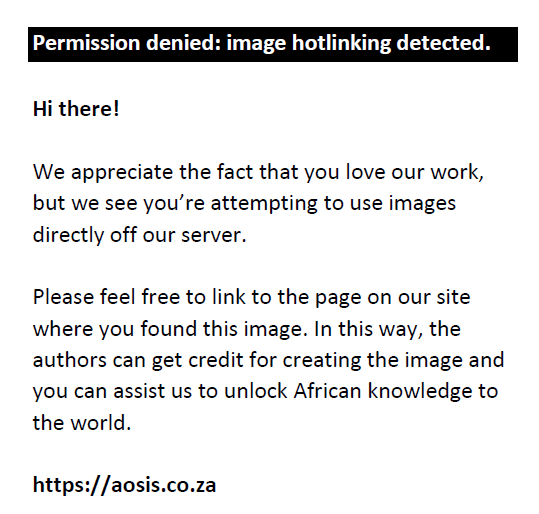 the function is at its maximum value of ∆+) where: the function is at its maximum value of ∆+) where:
Footnotes
1. The trading and banking books are accounting terms that refer to assets held by a bank that are regularly traded and the bank’s balance sheet assets expected to be held to maturity respectively.
2. The interaction of market and credit risk (IMCR) working group established by the BCBS give several examples where this can occur.
3. South African credit ratings relative to spreads and buVaR are provided in Figure 11.
4. Basel IV comprises: BCBS 306, BCBS 319, BCBS 347, BCBS 362, BCBS 303, BCBS 279, BCBS 352, BCBS 355, BCBS 325, BCBS 349 (PWC 2016).
|